本文缺少有力证明，且部分内容完全由个人添加，网上无法找到类似结论。可能存在错误。若读者发现错误可在评论区反馈。

Update 2022-03-05:

感谢 俊杰_Charles 的提醒，加入一个外边框可以避免情况 3，同时也处理了无穷大的情况。

大型 Hack 现场

恕我直言，现在网上很多 OJ 的半平面交模板题数据都太水了，而且有一些特殊的性质（下文中有提及），导致一些有缺陷的代码能够 AC。

半平面交主流模板（数据水），推荐模板（相对强一些），难用的模板（数据据说强，但是 POJ 的功能和使用体验……）。

主要有 3 个需要注意的地方：

  1. 半平面交大小为 0。

  2. 半平面交大小为 ∞\infty。

  3. 存在两条排完序后相邻的向量的极角差大于 π\pi。

对于主流模板而言，这三条都没有 hack，第一条没有 hack 是因为数据水，后两条因为模板本身具有特殊性质（给出了至少一个凸包）而不会出现。

情况 1，这种情况下如果有方向相反的向量且这两个向量的半平面无交集，那么在找交点时会出现呐呐呐 nan 或 -nan ，判一下 nan 或 -nan 即可，接下来有个我并不会证的结论：如果没有刚才那种情况，双端队列中最后会只有两个向量，不用特判，因为两个向量只会转化两个交点，面积就是 0。

情况 2 很好判，判一下做完半平面交后双端队列中相邻元素极角差是否有 ≥π\ge\pi 的即可。

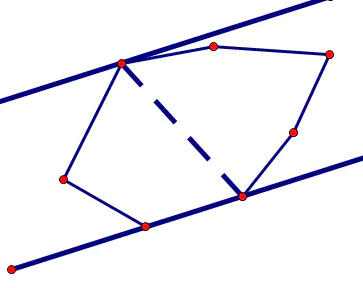
情况 3 的话比较复杂，也是一个我发现的 hack，目前我没有在网上找到题解提到过。hack 数据：

第一行一个整数 nn 表示向量个数，接下来 nn 行每行四个整数 x1,y1,x2,y2x_1,y_1,x_2,y_2 表示向量起点、终点横纵坐标。

1
2
3
4
3
2 4 0 0
2 4 4 0
4 1 0 2

图示：

图示

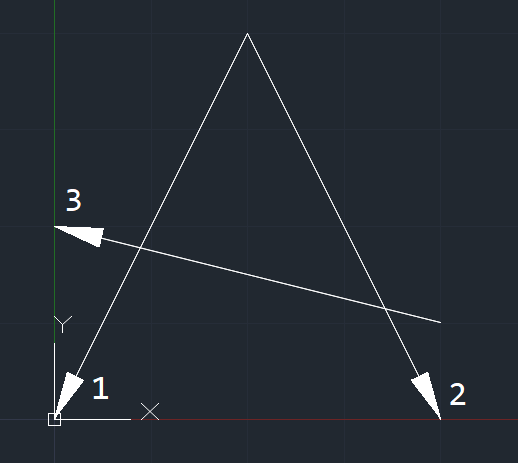
我目测遇到这种情况换一下 --ri 和 ++le 的顺序即可，但是没有严格证明（太菜了）。如果实在不行的话遇到这种情况 O(n)O(n) 处理一下也可以，因为显然只会遇到一次。

代码

代码中只有对于情况 1 的特判，没有 2、3 的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
struct Line {
    Point a, b;
    double angle;
    inline bool operator<(const Line sec) const {
        if (!cmp(angle, sec.angle)) {
            return area(a, b, sec.b) < 0;
        }
        return angle < sec.angle;
    }
} line[MAXn * MAXm + 10]; int cntline;
int le = 1, ri, que[MAXn * MAXm + 10];

signed main() {
    // ...
    sort(line + 1, line + 1 + cntline);
    for (int i = 1; i <= cntline; ++i) {
        if (!cmp(line[i].angle, line[i - 1].angle)) continue;
        while (le < ri && area(line[i].a, line[i].b, str_int_str(line[que[ri - 1]].a, line[que[ri - 1]].b, line[que[ri]].a, line[que[ri]].b)) <= 0) --ri;
        while (le < ri && area(line[i].a, line[i].b, str_int_str(line[que[le]].a, line[que[le]].b, line[que[le + 1]].a, line[que[le + 1]].b)) <= 0) ++le;
        que[++ri] = i;
    }
    while (le < ri - 1 && area(line[que[le]].a, line[que[le]].b, str_int_str(line[que[ri - 1]].a, line[que[ri - 1]].b, line[que[ri]].a, line[que[ri]].b)) <= 0) --ri;
    while (le < ri - 1 && area(line[que[ri]].a, line[que[ri]].b, str_int_str(line[que[le]].a, line[que[le]].b, line[que[le + 1]].a, line[que[le + 1]].b)) <= 0) ++le;
    // ...
    double ans = pol_area(point, cntpoint);
    if (isfinite(ans)) {
        printf("%.3lf\n", ans);
    } else {
        puts("0.000");
    }
}