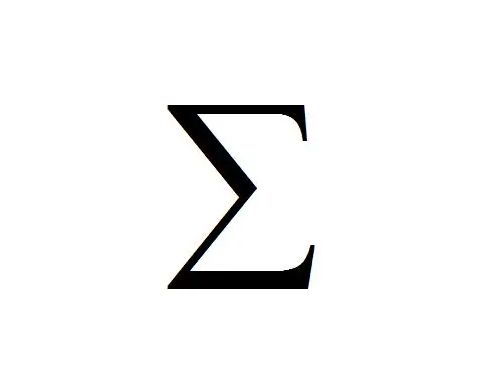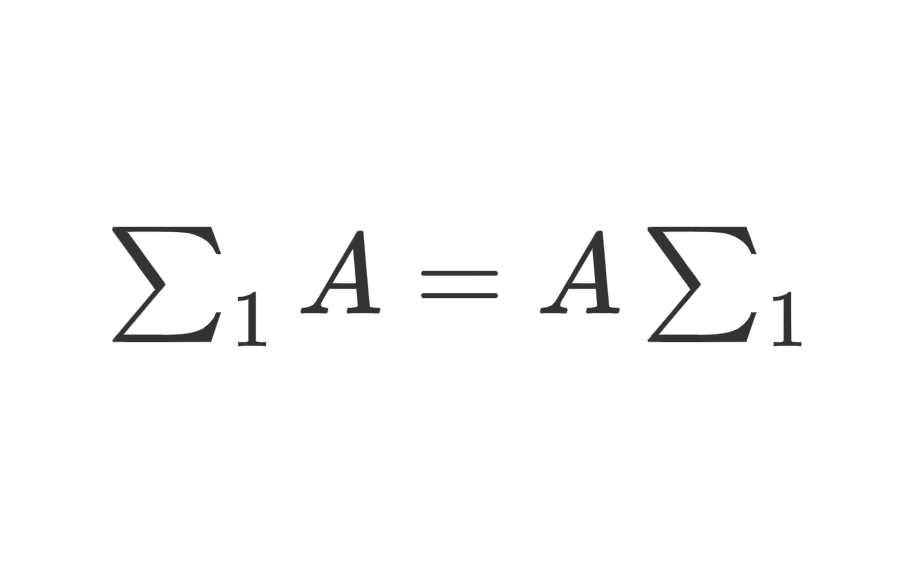莫比乌斯函数 & 莫比乌斯反演

一. 莫比乌斯函数

定义

设正整数 $n$，根据唯一分解定理分解为 $p_1^{c_1}p_2^{c_2}\cdots p_k^{c_k}$。

莫比乌斯函数可定义为 $\mu(n)=\begin{cases}0&(\exists i,c_i>1)\\(-1)^k&(else)\end{cases}$

性质

1. 莫比乌斯函数是积性函数，分类讨论可证得。

   因此我们可以用线性筛法筛莫比乌斯函数。

2. $\sum\limits_{d\mid n}\mu(d)=\begin{cases}1&(n=1)\\0&(n>1)\end{cases}$

   证明：

   1. $n=1$ 时，显然成立。

   2. $n>1$ 时：

      $$\begin{gather} \sum\limits_{d\mid n}\mu(d)=\sum\limits_{i=0}^{i\le c_1}\sum\limits_{j=0}^{j\le c_2}\cdots\sum\limits_{x=0}^{x\le c_k}\mu(p_1^ip_2^j\cdots p_k^x)\\ =\sum\limits_{i=0}^{i\le 1}\sum\limits_{j=0}^{j\le 1}\cdots\sum\limits_{x=0}^{x\le 1}\mu(p_1^ip_2^j\cdots p_k^x)\\ =\sum\limits_{i=0}^{i\le k}\binom{k}{i}(-1)^i\\ =(-1+1)^k\\ =0\\ \end{gather}$$

二. 莫比乌斯反演

第一定理

若 $F(n)=\sum\limits_{d\mid n}f(d)$，则 $f(n)=\sum\limits_{d\mid n}\mu(d)F(\dfrac{n}{d})$

证明：

$$\begin{gather} \text{若证}f(n)=\sum\limits_{d\mid n}\mu(d)F(\dfrac{n}{d})\\ \text{即证}f(n)=\sum\limits_{d\mid n}\mu(d)\sum\limits_{g\mid \frac{n}{d}}f(g)\\ \text{即证}f(n)=\sum\limits_{d\mid n}\sum\limits_{g\mid \frac{n}{d}}\mu(d)f(g)\\ \end{gather}$$

我们在这里需要证明 $\sum\limits_{d\mid n}\sum\limits_{g\mid \frac{n}{d}}=\sum\limits_{g\mid n}\sum\limits_{d\mid \frac{n}{g}}$。

什么情况下这两者等价呢？我们可以这样理解，每个 $\sum$，形如 $\sum\limits_{i=1}^{i\le n}$ 的也好，形如 $\sum\limits_{d\mid n}$ 的也罢，相当于是往后传递了若干次数，比如 $\sum\limits_{d\mid 6}$ 往后传递的数的集合为 $\{1,2,3,6\}$。两个 $\sum$ 就相当于传递了若干次数对。那么，设 $\sum\limits_{d\mid n}\sum\limits_{g\mid \frac{n}{d}}$ 向后传递的数对构成的集合为 $S_1$，$\sum\limits_{g\mid n}\sum\limits_{d\mid \frac{n}{g}}$ 向后传递的数对构成的集合为 $S_2$（其中数对的第一个位置表示 $d$，第二个位置表示 $g$）。如果我们能证明 $S_1=S_2$，我们就能证明 $\sum\limits_{d\mid n}\sum\limits_{g\mid \frac{n}{d}}=\sum\limits_{g\mid n}\sum\limits_{d\mid \frac{n}{g}}$。

因为每次向后传递的是一个数对，所以我们可以用一个矩阵来表示 $S_1$ 和 $S_2$。

因为 $d$ 严格单调，对于每个 $d$，$g$ 也严格单调，所以 $S_1$，$S_2$ 中均没有重复元素。我们可以用一个 $0/1$ 矩阵来表示 $S_1$ 和 $S_2$。

例如 $n=6$ 时 $\sum\limits_{d\mid n}\sum\limits_{g\mid \frac{n}{d}}$ 对应的 $0/1$ 矩阵：（每一行代表一个 $d$ 的值，每一列代表一个 $g$ 的值，省略 $0$）

$$\begin{bmatrix} &1&2&3&4&5&6\\ 1&1&1&1& & &1\\ 2&1& &1& & & \\ 3&1&1& & & & \\ 4& & & & & & \\ 5& & & & & & \\ 6&1& & & & & \\ \end{bmatrix}$$

根据这个例子，我们大概能猜出结论，这个矩阵一定是沿对角线对称的，我们来证明：

$$\begin{gather} \text{若}a[i][j]=1\\ \iff j\mid \dfrac{n}{i}\\ \iff i\mid \dfrac{n}{j}\\ \iff a[j][i]=1\\ \text{若}a[i][j]=0\\ \iff j\nmid \dfrac{n}{i}\\ \iff i\nmid \dfrac{n}{j}\\ \iff a[j][i]=0\\ \end{gather}$$

由此证得该矩阵沿对角线对称，由于这条性质，当 $\sum\limits_{d\mid n}\sum\limits_{g\mid \frac{n}{d}}$ 中 $d$ 与 $g$ 更换位置变成 $\sum\limits_{g\mid n}\sum\limits_{d\mid \frac{n}{g}}$ 后，表示成的矩阵不变（注意虽然公式中 $d,g$ 交换位置，但矩阵每一行仍代表一个 $d$ 的值，每一列仍代表一个 $g$ 的值。用向后传数对的方式理解，数对的第一个位置仍表示 $d$，第二个位置仍表示 $g$）。故 $S_1=S_2$，证得 $\sum\limits_{d\mid n}\sum\limits_{g\mid \frac{n}{d}}=\sum\limits_{g\mid n}\sum\limits_{d\mid \frac{n}{g}}$。

接着主线证明：

$$\begin{gather} \text{即证}f(n)=\sum\limits_{g\mid n}\sum\limits_{d\mid \frac{n}{g}}\mu(d)f(g)\\ \text{即证}f(n)=\sum\limits_{g\mid n}f(g)\sum\limits_{d\mid \frac{n}{g}}\mu(d)\\ \end{gather}$$

根据莫比乌斯函数的性质，发现右部的很多项都乘有 $0$，消去乘有 $0$ 的项可得：

$$\begin{gather} \text{即证}f(n)=f(n) \end{gather}$$

显然成立，证毕。

本证明过程由个人独自完成，且引入了数对和矩阵辅助证明，所以难免有些啰嗦，读者可以思考简化证明过程。

第二定理

若 $F(n)=\sum\limits_{n\mid d}f(d)$，则 $f(n)=\sum\limits_{n\mid d}\mu(\dfrac{d}{n})F(d)$

证明：

前面和第一定理推导过程相同，一直到这一步：

$$\begin{gather} \text{即证}f(n)=\sum\limits_{n\mid d}\sum\limits_{d\mid g}\mu(\dfrac{d}{n})f(g)\\ \end{gather}$$

这里开始和第一公式的推导不一样了。设 $d'=\dfrac{d}{n}$，则 $d=d'n$，带入得：

$$\begin{gather} \text{即证}f(n)=\sum\limits_{n\mid g}\sum\limits_{d'\mid \frac{g}{n}}\mu(d')f(g)\\ \end{gather}$$

解释：$n\mid d\mid g$ 所以 $g$ 一定能去遍 $n$ 的所有倍数，$d'$ 是 $\dfrac{d}{n}$，所以一定有 $d'\mid \dfrac{g}{n}$。

有人可能会问，这个怎么无法用证第一定理时那样用数对和矩阵的方式证明呢，因为确实 $\sum\limits_{n\mid d}\sum\limits_{d\mid g}\neq\sum\limits_{n\mid g}\sum\limits_{d\mid g}$，但是这里这两个 $\sum$ 号后面并不会用到 $d$ 的值，只会用到 $d'$，所以只需要保证 $d'$ 不变就行了。

对应到矩阵上来说，以 $n=2$ 举例，$\sum\limits_{n\mid d}\sum\limits_{d\mid g}$ 对应的矩阵：

$$\begin{bmatrix} &1&2&3&4&5&6\\ 1& & & & & & \\ 2& &1& &1& &1\\ 3& & & & & & \\ 4& & & &1& & \\ 5& & & & & & \\ 6& & & & & &1\\ \end{bmatrix}$$

$\sum\limits_{n\mid g}\sum\limits_{d\mid g}$：

$$\begin{bmatrix} &1&2&3&4&5&6\\ 1& &{\color{red}1}& &{\color{red}1}& &{\color{red}1}\\ 2& &1& &1& &1\\ 3& & & & & &{\color{red}1}\\ 4& & & &1& & \\ 5& & & & & & \\ 6& & & & & &1\\ \end{bmatrix}$$

可以看到两者中有不同之处的行所对应的 $d'\notin\mathbb{Z}$（$\dfrac{1}{2}$ 和 $\dfrac{3}{2}$）。

继续证明：

$$\begin{gather} \text{即证}f(n)=\sum\limits_{n\mid g}\sum\limits_{d'\mid \frac{g}{n}}\mu(d')f(g)\\ \end{gather}$$

接下来就和第一定理的过程完全一样了。

应用

如果有两个函数 $f(n)$ 和 $F(n)$，$F(n)$ 好求，$f(n)$ 不好求，而两者间又有 $F(n)=\sum\limits_{d\mid n}f(d)$ 或者 $F(n)=\sum\limits_{n\mid d}f(d)$ 的关系，可以使用莫反。

小技巧：遇到 $\sum\limits_{n\mid d}$ 的时候，可以设 $d'=\dfrac{d}{n}$，则 $d=d'n$，代入可得转化为 $\sum\limits_{d'=1}^{d'<\infty}$，这样变量就是连续的了。

两个重要结论

1. $\sum\limits_{d\mid n}\mu(d)=[n=1]$

   这条结论主要反着用。

2. $\sum\limits_{i=1}^{i\le n}\sum\limits_{d\mid i}=\sum\limits_{d=1}^{d\le n}\lfloor\dfrac{n}{d}\rfloor$