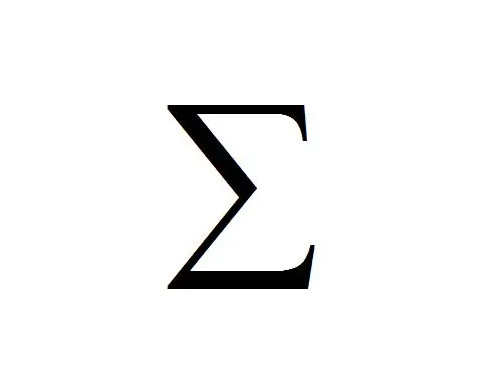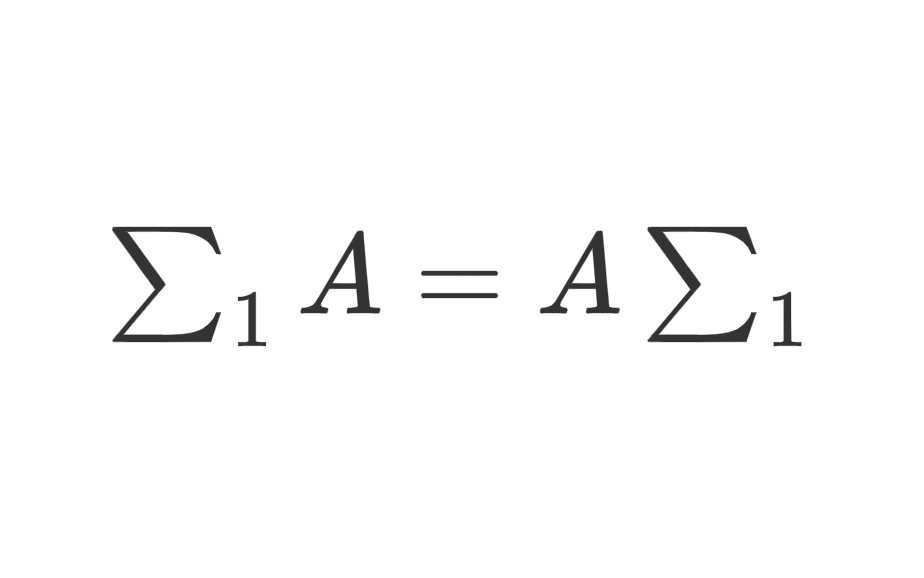广义容斥原理 & 二项式反演

本文仅作为整理思路，没有定理的严格证明。

定义

「容斥原理」和「广义容斥原理」这两章中，将使用以下定义。

$A$ ：一个包含 $n$ 个不同元素 $a_1,a_2\cdots a_n$ 的集合。注意 $n$ 的含义是集合大小。

$d_m$ ： $A$ 的子集中至少包含 $m$ 个元素的集合的数量。（ $A$ 的子集中大小 $\ge m$ 的集合的数量）

$f_m$ ： $A$ 的子集中恰好包含 $m$ 个元素的集合的数量。（ $A$ 的子集中大小 $= m$ 的集合的数量）

$g_{A'}$ ： $A'$ 是 $A$ 的子集，满足钦定选 $A'$ 中所有元素，其他元素无限制的条件的 $A$ 的子集的数量。

设所有包含元素 $a_i$ 的 $A$ 的子集所构成的集合为 $X_i$ ，以上定义用韦恩图表达如下：

白色代表这部分被算了 $0$ 次，红色代表这部分被算了 $1$ 次。

可以发现：

$g_{A'}=\left|\bigcap\limits_{a_i\in A'}X_i\right|$

还有一条性质：

$\sum\limits_{A'\subseteq A,|A'|=m}g_{A'}=\sum\limits_{i=m}^{i\le n}\binom{i}{m}f_i$

韦恩图表示如下：

蓝色代表这部分被算了 $3$ 次。

以集合的角度来理解容斥原理和广义容斥原理比较利于用韦恩图来数形结合理解。但是在 OI 题目中容斥原理的考察背景一般不是集合，而是有 $n$ 个性质，求恰好或至少满足 $m$ 个性质的方案数，而满足每条性质的方案数会有很多种，这点和集合不同，集合中每个元素如果被选择只有一种被选择的方法 ~~（好像是废话）~~。

容斥原理

我们都知道容斥原理可以求至少包含一个元素的子集数（或至少包含一条性质的方案数）：

$d_1=\sum\limits_{i=1}^{i\le n}(-1)^{i-1}\sum\limits_{A'\subseteq A,|A'|=i}g_{A'}$

集合论的形式：

$\left|\bigcup\limits_{i=1}^{i\le n}X_i\right|=\sum\limits_{i=1}^{i\le n}(-1)^{i-1}\sum\limits_{p_j<p_{j+1}}\left|\bigcap\limits_{j=1}^{j\le i}X_{p_j}\right|$

但是，容斥原理还有另一个形式，可以用于求恰好包含零个元素的子集数：

$\because f_0=|U|-d_1\\ \therefore f_0=\sum\limits_{i=0}^{i\le n}(-1)^i\sum\limits_{A'\subseteq A,|A'|=i}g_{A'}\\$

我们的广义容斥定理就是相对于这个公式的广义情况。

广义容斥定理

$f_m=\sum\limits_{i=m}^{i\le n}(-1)^{i-m}\binom{i}{m}\sum\limits_{A'\subseteq A,|A'|=i}g_{A'}$

可以看到普通容斥是广义容斥 $m=0$ 是的情况。

广义容斥定理是二项式反演的一种，和「定义」一章中的 $f$ 与 $g$ 的函数关系式互为反演关系。把广义容斥原理从几个二项式反演中单拎出来是因为我只理解这一个公式的组合意义 qwq，而且可以类比普通容斥。

二项式反演

以下的 $d,f,a$ 不按照「定义」一章中的意义，而表示任意数列或变量。

反演在线性代数下的理解很简单，就是逆矩阵：

$d_m=\sum\limits_{i=0}^{i\le m}A_{m,i}f_i \iff f_m=\sum\limits_{i=0}^{i\le m}B_{m,i}d_i$

相当于：

$\begin{bmatrix} d_0\\ d_1\\ \vdots\\ d_n \end{bmatrix}= A \begin{bmatrix} f_0\\ f_1\\ \vdots\\ f_n \end{bmatrix} \iff \begin{bmatrix} f_0\\ f_1\\ \vdots\\ f_n \end{bmatrix}= B \begin{bmatrix} d_0\\ d_1\\ \vdots\\ d_n \end{bmatrix}$

显然， $A=B^{-1}$ 。

以下所有反演公式均可通过矩阵的逆证明，故省略证明 ~~(太菜了)~~。

首先是广义容斥定理的二项式反演形式：

$d_m=\sum\limits_{i=m}^{\infty}\binom{i}{m}f_i\\ \iff f_m=\sum\limits_{i=m}^{\infty}(-1)^{i-m}\binom{i}{m}d_i\\$
其次是：

$d_m=\sum_{i=0}^{i\le m}\binom{m}{i}f_i\\ \iff f_m=\sum_{i=0}^{i\le m}(-1)^{m-i}\binom{m}{i}d_i\\$
然后是：

$d_m=\sum\limits_{i=m}^{\infty}(-1)^i\binom{i}{m}f_i\\ \iff f_m=\sum\limits_{i=m}^{\infty}(-1)^i\binom{i}{m}d_i\\$
最后是：

$d_m=\sum_{i=0}^{i\le m}(-1)^i\binom{m}{i}f_i\\ \iff f_m=\sum_{i=0}^{i\le m}(-1)^{i}\binom{m}{i}d_i\\$