题目传送门
一. 思路
首先进行离散化,将所有区间左右端点离散化,离散成 m m m
首先考虑朴素 DP,设 s e c l , r sec_{l,r} se c l , r l ∼ r l\sim r l ∼ r O ( n 3 ) O(n^3) O ( n 3 )
p r e i , j pre_{i,j} p r e i , j 1 ∼ i 1\sim i 1 ∼ i j j j
p r e i , j = max k = 1 k < i { p r e k , j + s e c k , i , p r e k , j − s e c k , i } pre_{i,j}=\max\limits_{k=1}^{k<i}\{pre_{k,j}+sec_{k,i},pre_{k,j-sec_{k,i}}\}
p r e i , j = k = 1 max k < i { p r e k , j + se c k , i , p r e k , j − se c k , i }
然后没有限制条件下的答案就是 max j = 1 n { min ( p r e m , j , j ) } \max\limits_{j=1}^n\{\min(pre_{m,j},j)\} j = 1 max n { min ( p r e m , j , j )}
s u f i , j suf_{i,j} s u f i , j i ∼ m i\sim m i ∼ m j j j p r e pre p re
d i , j d_{i,j} d i , j i ∼ j i\sim j i ∼ j
d l , r = max x = 1 m max y = 1 m { min ( x + s e c l , r + y , p r e l , x + s u f r , y ) } d_{l,r}=\max_{x=1}^{m}\max_{y=1}^{m}\left\{\min\left(x+sec_{l,r}+y,pre_{l, x}+suf_{r, y}\right)\right\}
d l , r = x = 1 max m y = 1 max m { min ( x + se c l , r + y , p r e l , x + s u f r , y ) }
要求编号为 i i i l e i le_i l e i r i i ri_i r i i
a n s i = max l = 1 l e i max r = r i i m { d l , r } ans_{i}=\max _{l=1}^{le_{i}} \max _{r=ri_{i}}^{m}\left\{d_{l, r}\right\}
an s i = l = 1 max l e i r = r i i max m { d l , r }
可以看到,整个解题过程的瓶颈就是 2 D / 2 D 2\operatorname{D}/2\operatorname{D} 2 D /2 D d i , j d_{i,j} d i , j O ( n 4 ) O(n^4) O ( n 4 ) l , r l,r l , r x x x y y y min ( x + s e c l , r + y , p r e l , x + s u f r , y ) \min\left(x+sec_{l,r}+y,pre_{l,x}+suf_{r,y}\right) min ( x + se c l , r + y , p r e l , x + s u f r , y ) y x ′ y'_x y x ′ p r e i pre_i p r e i j j j p r e i , j pre_{i,j} p r e i , j j j j
假设我们已求出了 y x ′ y'_{x} y x ′ y x + a ′ y'_{x+a} y x + a ′ a a a x + a x+a x + a x x x y y y x + s e c l , r + y x+sec_{l,r}+y x + se c l , r + y p r e l , x + s u f r , y pre_{l,x}+suf_{r,y} p r e l , x + s u f r , y y x ′ + b y'_x+b y x ′ + b b b b y x ′ y'_x y x ′ x x x x + s e c l , r + y x+sec_{l,r}+y x + se c l , r + y p r e l , x + s u f r , y pre_{l,x}+suf_{r,y} p r e l , x + s u f r , y
所以得出结论,y x + a ′ ≤ y x ′ y'_{x+a}\le y'_x y x + a ′ ≤ y x ′ > y x ′ >y'_x > y x ′ x x x x + a x+a x + a
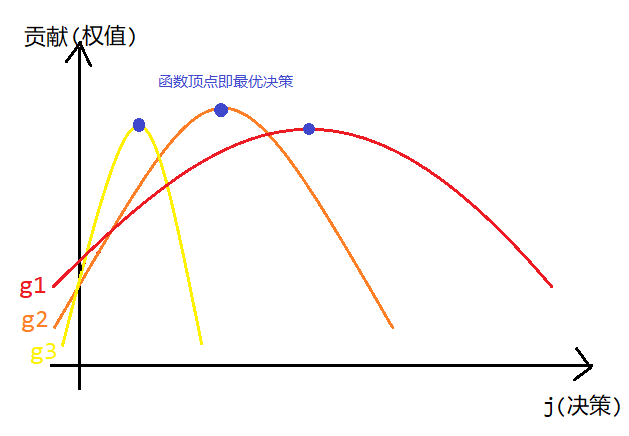
设 g l , r , x ( y ) = min ( x + s e c l , r + y , p r e l , x + s u f r , y ) g_{l,r,x}(y)=\min\left(x+sec_{l,r}+y,pre_{l,x}+suf_{r,y}\right) g l , r , x ( y ) = min ( x + se c l , r + y , p r e l , x + s u f r , y ) l l l r r r g x ( y ) g_x(y) g x ( y ) x + s e c l , r + y = p r e l , x + s u f r , y x+sec_{l,r}+y=pre_{l,x}+suf_{r,y} x + se c l , r + y = p r e l , x + s u f r , y g x ( y ) g_x(y) g x ( y )
请注意现在的一个函数 对应的是一个状态 ,横坐标 对应的是决策 。
于是我们尝试画出这个图象,刚才我们已经证出两条性质:
o p op o p g i ( j ) g_i(j) g i ( j )
(图像仅供参考,不代表实际上就长这样,该图象只显示出了对解题有用的特征)
o p op o p g i ( j ) g_i(j) g i ( j )
根据这两条性质,可以直接用一个指针从右往左扫,向上“爬坡”,到顶点后就记录这个值,并转到下一条函数:
转移的代码实现:
1 2 3 4 5 6 7 8 9 10 for (int i = 1 ; i <= cntmap; ++i) { for (int j = i + 1 ; j <= cntmap; ++j) { int y = n; for (int x = 0 ; x <= n; ++x) { while (y && min (x+sec[i][j]+y,pre[i][x]+suf[j][y])<=min (x+sec[i][j]+y-1 ,pre[i][x]+suf[j][y-1 ])) --y; d[i][j] = max (d[i][j], min (x + sec[i][j] + y, pre[i][x] + suf[j][y])); } ans = max (ans, d[i][j]); } }
二. 细节
很重要,也很致命 。
向上“爬坡”时,我们需要比较指针当前位置和指针下一个位置作为决策哪一个更优,有人会用 <=,有人会用 <,如果你用 <,你会获得 0 {\color{Red}0} 0
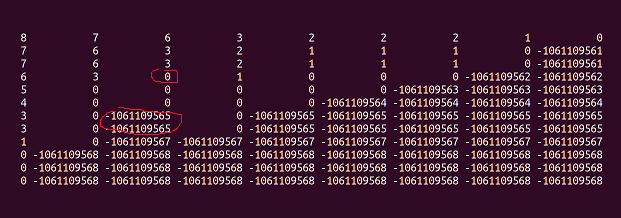
我们的代码实现和理论是有一定区别的,通常会自动忽略一些不可能是最优的决策,以本体为例,比如有这样的一个“区间”,里面刚好包含两个重合的区间(还记得加和不加引号的“区间”分别代表什么吗?):
我们当然不会舍弃这两个区间其中任意一个,因为完全可以不舍弃。但确实有一种选择是舍弃其中一个,虽然这样不优,但我们在代码中做的是将所选“区间”中区间的数量作为权值 s e c sec sec s e c sec sec s u f suf s u f
可以看到,s u f suf s u f s u f suf s u f
注意 :上面这个函数表示的是数组里存的值,是用计算机算出来的值,而非实际的函数,如果函数确实就长这样他根本就满足不了双指针优化的前提条件!
因为满足 s u f i ≥ s u f i + a suf_i\ge suf_{i+a} s u f i ≥ s u f i + a a a a
填坑代码实现:
1 2 3 4 5 6 7 8 9 10 11 for (int i = 1 ; i <= cntmap; ++i) { for (int j = n - 1 ; ~j; --j) { pre[i][j] = max (pre[i][j], pre[i][j + 1 ]); } } for (int i = 1 ; i <= cntmap; ++i) { for (int j = n - 1 ; ~j; --j) { suf[i][j] = max (suf[i][j], suf[i][j + 1 ]); } }
三. 代码
完整代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 #include <bits/stdc++.h> using namespace std;const int MAXn = 2e2 ;template <typename T> inline void read (T &a) register char c;while (c = getchar (), c < '0' || c > '9' );register T x (c - '0' ) while (c = getchar (), c >= '0' && c <= '9' ) {x = (x << 1 ) + (x << 3 ) + (c ^ 48 );}a = x; } template <typename T, typename ...Argv>inline void read (T &n, Argv &...argv) read (n), read (argv...); } int n;int cntmap, mapup[MAXn * 2 + 10 ]; map<int , int > mapdown;int le[MAXn + 10 ], ri[MAXn + 10 ];int sec[MAXn * 2 + 10 ][MAXn * 2 + 10 ];int pre[MAXn * 2 + 10 ][MAXn + 10 ], suf[MAXn * 2 + 10 ][MAXn + 10 ], d[MAXn * 2 + 10 ][MAXn * 2 + 10 ], ans;signed main () read (n); for (int i = 1 , l, len, r; i <= n; ++i) { read (l, len); r = l + len; le[i] = l; ri[i] = r; mapup[++cntmap] = l; mapup[++cntmap] = r; } sort (mapup + 1 , mapup + 1 + cntmap); cntmap = unique (mapup + 1 , mapup + 1 + cntmap) - (mapup + 1 ); for (int i = 1 ; i <= cntmap; ++i) { mapdown[mapup[i]] = i; } for (int i = 1 ; i <= n; ++i) { le[i] = mapdown[le[i]]; ri[i] = mapdown[ri[i]]; } for (int i = 1 ; i <= cntmap; ++i) { for (int j = i + 1 ; j <= cntmap; ++j) { for (int k = 1 ; k <= n; ++k) { if (le[k] >= i && ri[k] <= j) ++sec[i][j]; } } } memset (pre, 0xc0 , sizeof pre[1 ][0 ] = 0 ; for (int i = 2 ; i <= cntmap; ++i) { for (int j = 0 ; j <= n; ++j) { for (int k = 1 ; k < i; ++k) { pre[i][j] = max (pre[i][j], max (pre[k][j - sec[k][i]], pre[k][j] + sec[k][i])); } } } for (int i = 1 ; i <= cntmap; ++i) { for (int j = n - 1 ; ~j; --j) { pre[i][j] = max (pre[i][j], pre[i][j + 1 ]); } } memset (suf, 0xc0 , sizeof suf[cntmap][0 ] = 0 ; for (int i = cntmap - 1 ; i; --i) { for (int j = 0 ; j <= n; ++j) { for (int k = cntmap; k > i; --k) { suf[i][j] = max (suf[i][j], max (suf[k][j - sec[i][k]], suf[k][j] + sec[i][k])); } } } for (int i = 1 ; i <= cntmap; ++i) { for (int j = n - 1 ; ~j; --j) { suf[i][j] = max (suf[i][j], suf[i][j + 1 ]); } } for (int i = 1 ; i <= cntmap; ++i) { for (int j = i + 1 ; j <= cntmap; ++j) { int y = n; for (int x = 0 ; x <= n; ++x) { while (y && min (x + sec[i][j] + y, pre[i][x] + suf[j][y]) <= min (x + sec[i][j] + y - 1 , pre[i][x] + suf[j][y - 1 ])) --y; d[i][j] = max (d[i][j], min (x + sec[i][j] + y, pre[i][x] + suf[j][y])); } ans = max (ans, d[i][j]); } } printf ("%d\n" , ans); for (int i = 1 ; i <= n; ++i) { int partans = 0 ; for (int j = le[i]; j; --j) { for (int k = ri[i]; k <= cntmap; ++k) { partans = max (partans, d[j][k]); } } printf ("%d\n" , partans); } }