一. 思路

0. 前置知识：割点，v-dcc（再说一遍，无向图有的是双连通分量，没有强连通分量一说！）。

​ 这里推荐几道模板题，学习 Tarjan 建议把他们都 A 了：

  1. dcc 割边：Luogu Std。

  2. dcc 割点：Luogu Std。

  3. e-dcc：Luogu Std。

  4. v-dcc：Luogu Std。

  5. scc：Luogu Std。

  6. scc 缩点：Luogu。

（没有找到双连通分量的缩点模板，知道的小伙伴欢迎在评论中补充）

蓝书上这部分讲的很详细。

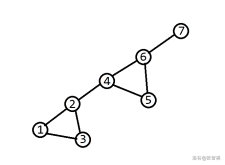
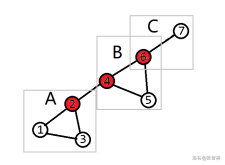
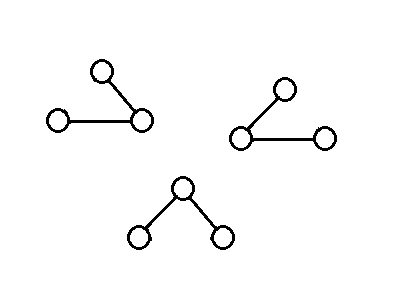
那么接下来我们以这个图为例讲解此题：

命名三个双连通分量为：A，B，C。红色的为割点。

1. 一个包含一个割点的双连通分量（A，C）

  1. 非割点坍塌：

    没有关系，比如 A 中 1 号点坍塌，3 号点中的人可以来到割点（2 号点），然后去往其他双连通分量中的出口逃生。

  2. 割点坍塌：

    比如 2 号塌了，1 号和 3 号中就必须有一个出口。

综上，对于包含一个割点的双连通分量，需要建 11 个出口，方案数为 size⁡−1\operatorname{size} - 1。（size⁡\operatorname{size}：该 dcc 大小）。

2. 一个包含两个及以上个割点的双连通分量（B）

  1. 非割点坍塌：（同 1 - 1）

  2. 割点坍塌：

    这次情况不同了，塌了一个割点，还有至少一个割点可以供里面的工人离开这个 dcc。

综上，对于包含两个及以上个割点的双连通分量，根本无需建出口。

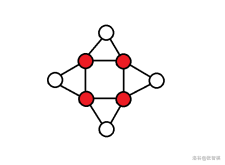
看到这里，很多人有 问题 了：如果全是包含两个及以上个割点的 dcc，所有人总想着往其他 dcc 跑，其他 dcc 却也没出口怎么办。那么恭喜你，这种情况根本不可能成立。比如有一圈像 B 一样的 dcc 拼在一起：

但再仔细看，一当形成环，割点就直接没有了，也就是说上图 4 个红色点都应该是白色的，这就是第三种情况（待会要讲）。

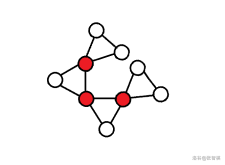
而如果环不合拢，两端必然存在包含一个割点的 dcc，也就自然能成功逃离：

3. 环

如果是一个环，看上去建一个出口就行了，但还要考虑出口坍塌的情况！所以需要建 22 个出口。方案数为 C⁡size⁡2=size⁡×(size⁡−1)2\operatorname{C}^2_{\operatorname{size}} = \dfrac{\operatorname{size} \times (\operatorname{size} - 1)}{2}。

4. 最终结果

  1. 出口数：将所有 dcc 建的出口数相加。
  2. 方案数：将所有 dcc 的方案数相乘。（乘法原理）

二. 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
#define re register
#define int long long
const int MAXn = 5e4;
const int MAXm = 3e5;

template <class T>
inline void read(T& a) {
    re char c; while (c = getchar(), c < '0' || c > '9'); re T x(c - '0'); while (c = getchar(), c >= '0' && c <= '9') { x = x * 10 + c - '0'; }a = x;
}

int head[MAXn + 10], cntnex, nex[MAXm * 2 + 10], to[MAXm * 2 + 10];
void Insert(int u, int v) {
    nex[++cntnex] = head[u];
    head[u] = cntnex;
    to[cntnex] = v;
}

int top, stk[MAXn + 10], cntdcc;
vector<int> dcc[MAXn + 10];
bool is[MAXn + 10];
int root, cntdfs, dfs[MAXn + 10], low[MAXn + 10];

void Init() {
    cntnex = top = root = cntdfs = 0;
    memset(head, 0, sizeof(head));
    memset(nex, 0, sizeof(nex));
    memset(to, 0, sizeof(to));
    memset(stk, 0, sizeof(stk));
    memset(is, 0, sizeof(is));
    memset(dfs, 0, sizeof(dfs));
    memset(low, 0, sizeof(low));
    for (re int i = 1; i <= cntdcc; ++i) {
        dcc[i].clear();
    }
    cntdcc = 0;
}

void Tarjan(int cur) {
    int times = 0;
    dfs[cur] = low[cur] = ++cntdfs;
    if (!head[cur]) {
        ++cntdcc;
        dcc[cntdcc].push_back(cur);
        return;
    }
    stk[++top] = cur;
    for (re int i = head[cur]; i; i = nex[i]) {
        if (!dfs[to[i]]) {
            Tarjan(to[i]);
            low[cur] = min(low[cur], low[to[i]]);
            if (dfs[cur] <= low[to[i]]) {
                ++times;
                if (cur != root || times >= 2) {
                    is[cur] = 1;
                }
                ++cntdcc;
                int instk;
                do {
                    instk = stk[top--];
                    dcc[cntdcc].push_back(instk);
                } while (instk != to[i]);
                dcc[cntdcc].push_back(cur);
            }
        }
        else {
            low[cur] = min(low[cur], dfs[to[i]]);
        }
    }
}

int n, m;
signed main() {
    int T = 0;
    while (~scanf("%lld", &m)) {
        if (m == 0) {
            break;
        }
        ++T;
        n = 0;
        Init();
        for (re int i = 1, u, v; i <= m; ++i) {
            read(u), read(v);
            n = max(n, u); n = max(n, v);
            if (u == v) {
                continue;
            }
            Insert(u, v); Insert(v, u);
        }
        for (re int i = n; i; --i) {
            if (!dfs[i]) {
                root = i;
                Tarjan(i);
            }
        }
// 除核心以外的都是纯板子
// ---------------核心---------------
        int ans1 = 0, ans2 = 1;
        for (re int i = 1; i <= cntdcc; ++i) {
            int cnt = 0;
            for (re vector<int>::iterator j = dcc[i].begin(); j != dcc[i].end(); ++j) {
                if (is[*j]) {
                    ++cnt;
                }
            }
            if (cnt == 1) {
                ++ans1;
                ans2 *= dcc[i].size() - 1;
            } else if (cnt == 0) {
                ans1 += 2;
                ans2 *= dcc[i].size() * (dcc[i].size() - 1) / 2;
            }
        }
// ---------------核心---------------
        printf("Case %lld: %lld %lld\n", T, ans1, ans2);
    }
}