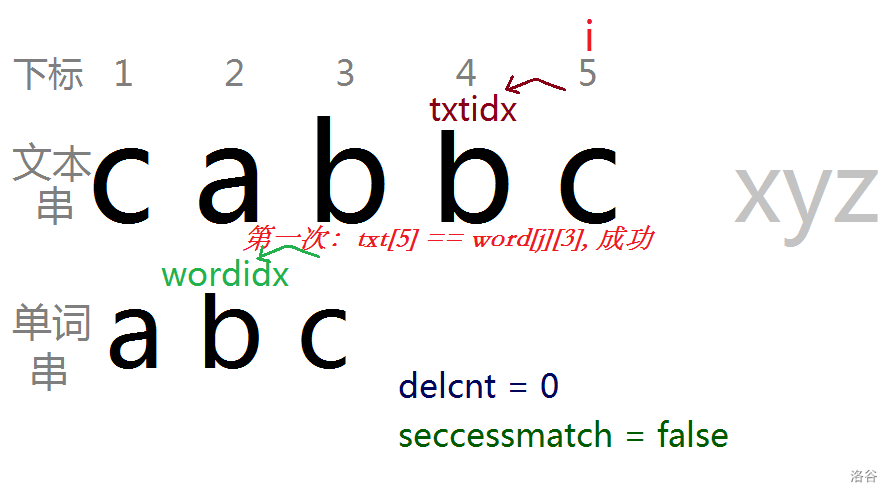Luogu P2432 zxbsmk爱查错

P2432 zxbsmk爱查错

一. 审题：

1.已知&输入：

• 给出一个长度为 $L$ 的文本串。
• 给出 $W$ 个单词串。

2.目标&输出：

• 在文本串中删除尽量少的字母使得文本串只有由词串构成，输出这个最少删除的字母数。

二. 思路

1. 思考解法

• 文本串后面的内容不会影响文本串前半部分的最优解，符合无后效性。
• 若把文本串右端位置作为状态，文本串右端位置较靠右的状态需要通过文本串右端位置较靠左的状态得到（如 $d_i$ 需要通过 $d_0 \dots d_{i-1}$ 的其中之一得到），符合子问题重叠性。

所以考虑DP。

2. 确定状态转移方程

$d_i$：前 $i$ 个子母的文本串中最少删除的字母数。

$txtidx$：用该第 $j$ 个单词串匹配前 $i$ 个子母的文本串，匹配完时文本串的下标。（3. 中有详解）

$delcnt$：用该第 $j$ 个单词串匹配前 $i$ 个子母的文本串，匹配过程中失配的次数。（3. 中有详解）

$seccessmatch$：用该第 $j$ 个单词串匹配前 $i$ 个子母的文本串，是否匹配成功。（3. 中有详解）

综上所述，状转方程：$d_i=\min_{j=1}^{W}\begin{cases}d_{i-1}+1&(seccessmatch=false)\\d_{txtidx}+delcnt&(seccessmatch=true)\end{cases}$

3.细节&详解

反正跟字符串有关题的题解，没图我是看不懂。

比如文本串是 cabbcxyz ，我们现在正在求 $d_5$ （$i=5$） 用其中一个单词串 abc 匹配，用某个单词匹配时不用管其他单词。

初始时把 $txtidx$ 设为 $i$ （也就是 $5$），$wordidx$ 设为单词长度， $delcnt$ 设为 $0$ 。（注意 $delnum$ 不是整个文本串删去的字母个数，而是当前情况下匹配过部分的文本串的删去字母个数。3. 中有详解）

初始时：

第一次匹配后：

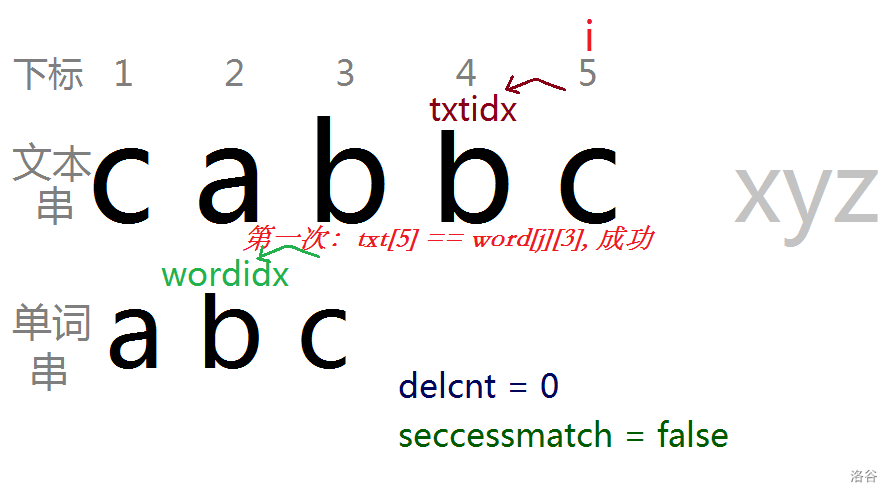
第二次匹配后：

第三次匹配后：

第四次匹配后：

三. 代码

代码中有比较详细的注释。

#include<bits/stdc++.h>
using namespace std;
const int MAXwordcnt = 600;//单词数量最大值 
const int MAXwordlen = 25;//单词长度最大值 
const int MAXtxtlen = 300;//文本长度最大值 

int wordcnt/*单词数量*/, txtlen/*文本长度*/;
char word[MAXwordcnt + 10][MAXwordlen + 10]/*单词*/, txt[MAXtxtlen + 10]/*文本*/;
int d[MAXtxtlen];//DP数组 
int main() {
    scanf("%d %d", &wordcnt, &txtlen);
    scanf("%s", txt + 1);
    for (int i = 1; i <= wordcnt; ++i) {
        scanf("%s", word[i] + 1);
    }
    d[0] = 0;
    for (int i = 1; i <= txtlen; ++i) {
        d[i] = d[i - 1] + 1;//如果没有单次得以再次位置匹配，需要删除的单词数++ 
        for (int j = 1; j <= wordcnt; ++j) {
            int wordidx = strlen(word[j] + 1);//此时单词串的下标
            int txtidx;//此时文本串的下标
            int delcnt = 0;//当前情况下匹配过部分的文本串的删去字母个数
            bool seccessmatch = 0;//是否匹配成功
            for (txtidx = i; txtidx >= 1; --txtidx) {
                if (wordidx == 0) {//wordidx == 0代表单词已经匹配完了 
                    seccessmatch = 1;
                    break;
                }
                if (txt[txtidx] == word[j][wordidx]) {//如果单词串与文本串在该位置相同... 
                    --wordidx;						  //那么匹配下一位 
                } else {							  //否则...
                    ++delcnt;						  //需要删的个数++ 
                }
            }
            if (wordidx == 0) {//wordidx == 0代表单词已经匹配完了 
                seccessmatch = 1;
            }
            if (seccessmatch) {						 //如果成功匹配... 
                d[i] = min(d[i], d[txtidx] + delcnt);//转移状态
            }
        } 
    }
    printf("%d", d[txtlen]);
}